フラクタル次元
無限の世界には，有限の世界と違って，
我々が予想もつかないような不思議なことが起こる。
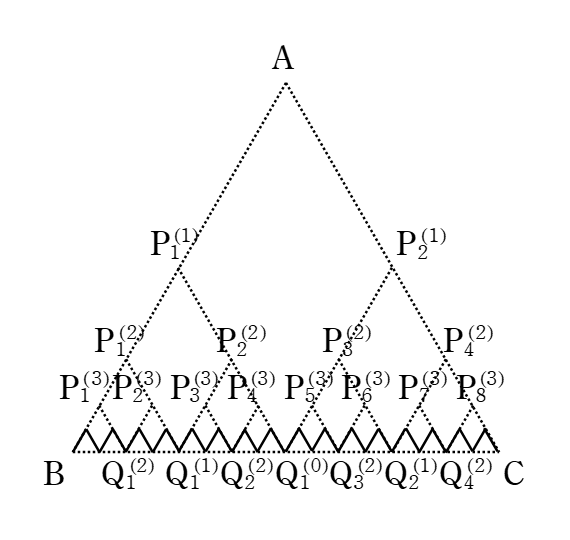
正三角形 \(\rm{ ABC }\) において，\( \rm{ AB, AC }\) の中点をそれぞれ
\( \rm{ P_{1}^{(1)}, P_{2}^{(1)} } \) とし，
\( \rm{ BC } \) の中点を \( \rm{ Q_{1}^{(0)} } \) とする。次に，
\( \rm{ P_{1}^{(1)}B, P_{1}^{(1)}Q_{1}^{(0)}, P_{2}^{(1)}Q_{1}^{(0)}, P_{2}^{(1)}C } \)の中点をそれぞれ
\( \rm{ P_{1}^{(2)}, P_{2}^{(2)}, P_{3}^{(2)}, P_{4}^{(2)} } \) とし，
\( \rm{ BQ_{1}^{(0)}, Q_{1}^{(0)}C } \) の中点をそれぞれ
\( \rm{ Q_{1}^{(1)}, Q_{2}^{(1)} } \) とする。
このとき，関係
\begin{eqnarray}
\rm{AB} + \rm{AC}
&=& \rm{P_{1}^{(1)}B} &+& \rm{P_{1}^{(1)}Q_{1}^{(0)}} + \rm{P_{2}^{(1)}Q_{1}^{(0)}} + \rm{P_{2}^{(1)}C } \nonumber \\
&=& \rm{P_{1}^{(2)}B} &+& \rm{P_{1}^{(2)}Q_{1}^{(1)}} + \rm{P_{2}^{(2)}Q_{1}^{(1)}} + \rm{P_{2}^{(2)}Q_{1}^{(0)}} \nonumber \\
& & &+& \rm{P_{3}^{(2)}Q_{1}^{(0)}} + \rm{P_{3}^{(2)}Q_{2}^{(1)}} + \rm{P_{4}^{(2)}Q_{2}^{(1)}}
+ \rm{P_{4}^{(2)}C} \nonumber \\
\end{eqnarray}
が成立する。
この操作を何回繰り返しても，折れ線の長さの和は常に一定で辺 \(\rm{AB}\)と \(\rm{AC}\) の長さの和に等しい。
この操作を無限に繰り返すと，折れ線は辺 \(\rm{BC}\) と一致するように埋め込まれる。すなわち，
「\(\rm{AB + AC = BC}\)」という関係が成立する。
無限の世界では「\(\rm{ 1+1=1 }\)」は正しい等式である。（? ? ?）
これに少し関連する話として，フラクタル次元について紹介しよう。
次元とは，「点の位置を表すのに必要な座標の数」のことである。
すなわち，直線は1次元，平面は2次元，空間は3次元ということになる。
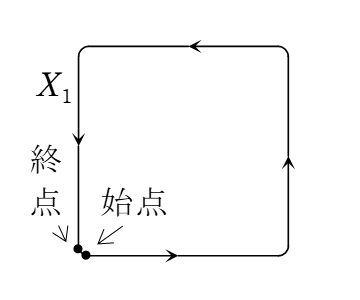
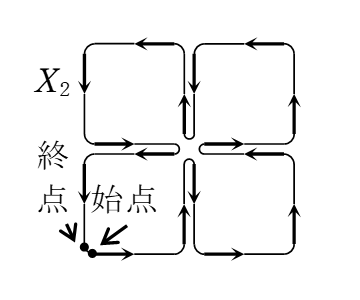
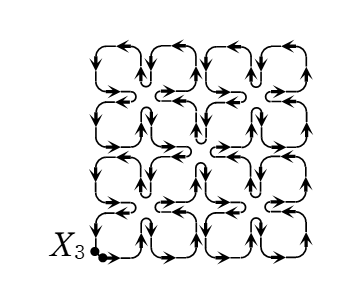
今から1世紀ほど前（1890年），ペアノは“ペアノ曲線”と呼ばれる正方形を埋め尽くす連続な曲線を発見した。（図１～３参照）
ペアノ曲線は曲線だから“１次元”なのか，それとも正方形を埋め尽くしているのだから“２次元”なのか。
複雑に入り組んだ線，例えばフラクタル図形に対して，次元（相似次元）をどう定義すべきか。
１次元で線分を2倍にすると長さは２倍，2次元で正方形を２倍にすると面積は \(2^{2}\) 倍，
３次元で立方体を２倍にすると体積は \(2^{3}\) 倍になる。
これを一般化して，次のように次元をとらえることができよう。
ある図形を \(r\) 倍に相似拡大すると，その大きさが \(r^d\) 倍になる指数 \(d\) を，その図形の次元と定めよう。
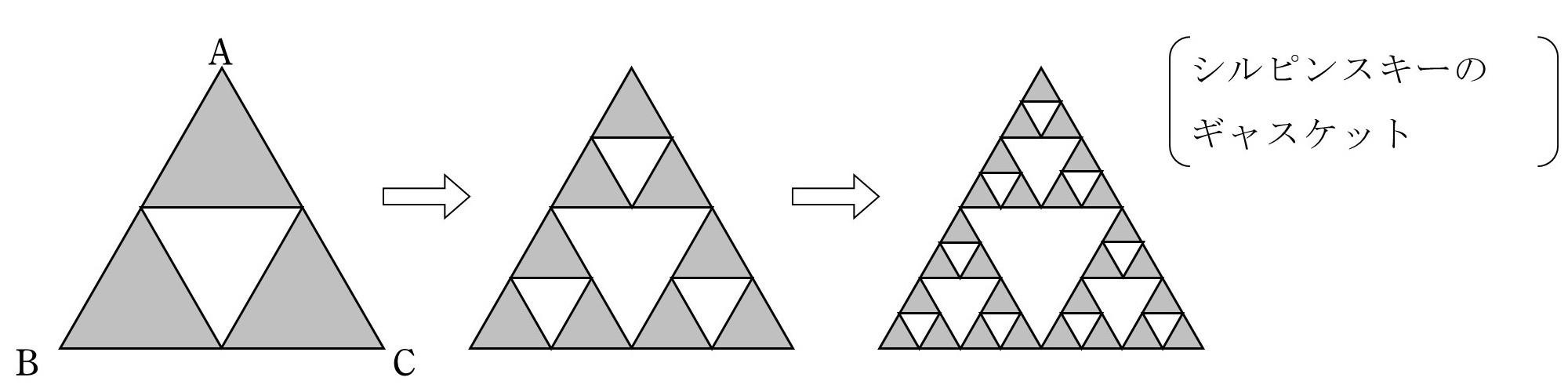
上図のような図形を考える。
まず，正三角形 \(\rm{ ABC }\) を考える。
この正三角形から各辺の中点を結んでできる正三角形を１個取り除いて，３つの正三角形からなる図形を考える。
次にその３つの正三角形から各辺の中点を結んでできる正三角形を3個取り除いて９個の小さな正三角形からなる図形を考える。
この操作を繰り返してできる図形を考える。
この図形を \(X\) とする。この図形の面積は \(0\) である。
実際に，△\(\rm{ABC}\) の面積を \(S\) とすれば，
取り除かれた正三角形の面積の総和は
\begin{eqnarray}
\frac{1}{4} S + 3 \cdot \left(\dfrac{1}{4}\right)^2 S + 3^2 \cdot \left(\dfrac{1}{4}\right)^3 S + \cdots
= \frac{\frac{1}{4} S }{1-\dfrac{3}{4}} = S \nonumber\\
\end{eqnarray}
である。
この図形 \(X\)を２倍に拡大すると，大きさが３倍になるので，\(2^d=3\)，すなわち
\begin{eqnarray}
d = \log_2 3 = \dfrac{log_{10}3}{log_{10}2} = 1.5849625 \cdots \nonumber \\
\end{eqnarray}
である。
この次元の定義は，相似な図形に限る。
もっと一般的な次元の定義とし，ハウスドルフ次元がある。
一般に，整数とは限らない次元をフラクタル次元という。
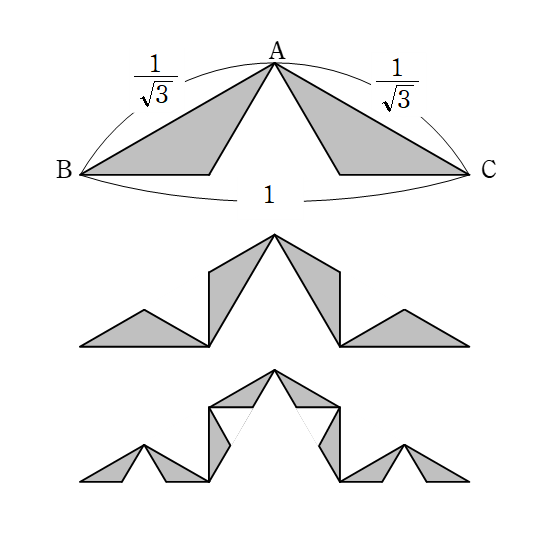
右図のように，二等辺三角形 \(\rm{ABC}\) から順に正三角形を \(1個，2個，2^2個，2^3個， \cdots \) を取り除いてできるコッホ曲線は，
\((\sqrt{3})^d = 2\) より，その次元が \(d= \dfrac{log_{10}4}{log_{10}3} =1.26 \cdots \) である。
このようにして，いろいろなフラクタル図形の次元が計算できる。
1次元と2次元の間に新しい次元を考えるというアイディアがすばらしい。
